https://terms.naver.com/search.nhn?query=%EB%AF%B8%EB%B6%84&searchType=text&dicType=&subject=
미분 수학산책
미분은 알고 보면 별 것이 아니다. 접선을 구하자는 것이 바로 미분이기 때문이다. 물론 접선의 기울기, 즉 미분 계수를 구하는 과정에서 함수의 극한,
미분
혹은 수열의 극한을 계산해야 하는데 다소 번거로운 경우가 많아 만만한 일만은 아니다.
https://terms.naver.com/list.nhn?cid=58944&categoryId=58970
미분 [differential, 微分] 두산백과
함수의 아주 작은 변화값을 나타내는 무한소를 말한다. 함수 f(x)가 미분가능인 경우에 y=f(x)라 놓고 x와 y의 증분을 각각 Δx, Δy로 놓으면, 이다. 이 식은 Δy=f'(x)Δx+εΔx로 고쳐 쓸 수 있다. 그리고 εΔx는 Δx보다 고위의 무한소이므로 Δy의 주부분은 f'(x)Δx로 생각할 수 있고, 이것...
관련정보도함수, 로그미분법, 미분법, 부정적분, 전미분, 편미분
https://terms.naver.com/list.nhn?cid=40942&categoryId=40942
미분 수학백과
미분 (differential / derivation / differentiation) 미분이란 어떤 운동이나 함수의 순간적인 움직임을 서술하는 방법이다. 어떤 함수의 미분이란 그것의 도함수를 도출해내는 과정을 말한다. 미분 공식을 이용하면 다항함수, 유리함수, 지수함수, 로그함수, 삼각함수 등 우리가 알고 있는 다양한 함수들에 대해서 그 도함수를 어렵지 않게 구할 수 있다. 자...
https://terms.naver.com/list.nhn?cid=60207&categoryId=60207
미분 [différentielle] 철학사전
미분은 아주 잘게 나누는 것이다. 공간을 아주 잘게 나누어서 아주 얇은 공간이 되는 게 아니라 그냥 하나의 면이 되도록 만드는 것, 또 면을 아주 잘게 나누어서 선으로······만드는 것을 말한다. 그래서 3차원이 2차원이 되고 또 1차원으로 되는 것, 즉 차수가 낮아진다. 적분(intégral)은 그 반대로, 선을 무한히 많이 더해서 면적을 만들고 또 면을 무한히...
https://terms.naver.com/list.nhn?cid=41978&categoryId=41985
미분 [微分, Differentialkalkül] 헤겔사전
헤겔은 『논리의 학』에서 상세히 미분론을 전개하고 있지만('정량의 무한성'에 대한 주해), 이것은 헤겔에게 있어 미적분(뉴턴, 라이프니츠 이래의 해석학)이 수학에서 사용되는 무한('수학적 무한')의, 철학적으로 그 의의가 가장 깊은 사례를 제공하고 있었기 때문이라고 말할 수 있다...
관련정보비례, 무한, 라이프니츠
https://terms.naver.com/list.nhn?cid=41908&categoryId=41971
미분 [fine particles, 微粉] 환경공학용어사전
분체를 구성하는 입자에는 육안으로 보이는 것에서 콜로이드 입자까지 여러 가지 크기의 것이 있다. 그 중에서 입경 40㎛ 이상의 것을 조분, 40㎛ 이하 수 ㎛까지를 미분, 그 이하를 초미분이라 한다. 입경 1㎜ 이상의 것은 입체라 하며, 분체와 구분한다. 주행중인 자동차의 배기 가스 중에 포함된 납 화합물의 입경은 0.01~1㎛, 대기 오염물로 보이는...
https://terms.naver.com/list.nhn?cid=42361&categoryId=42361
정적분 폐구간 [a,b]를 가지는 유계인 함수 f를 무한히 구분하여 극한값 s에 수렴하면, s를 f의 a에서 b까지의 정적분이라고 함
정적분 Basic 고교생을 위한 수학공식 활용사전
[ 1. 정적분] f(x)의 부정적분의 하나를 F(x)라 하면 정적분 이다. a는 정적분의 아래끝, b는 위끝이고, 크기 순서는 상관없다. [ 2. 적분과 미분의 관계] 함수 f(x)가 구간 [a, b]에서 연속이고 a ≦ x ≦ b일 때 [예문 1] [예문 2] [예문 3]
https://terms.naver.com/list.nhn?cid=42427&categoryId=42427
정적분 공식 통합논술 개념어 사전
[ 1. 교과서 속 주개념] [ 1) 정적분과 미분의 관계] (1) (2) [ 2) 정적분의 성질] (1) (2) (3) (단, k는 상수) (4) (복호동순) (5) (단, c는 임의의 실수) [ 3) 정적분의 응용] (1) 함수 f(x)가 기함수(f(-x)...
교과단원수학 Ⅱ, Ⅴ. 적분법, Ⅴ-1 다항함수의 적분법
https://terms.naver.com/list.nhn?cid=43669&categoryId=43669
미분 [米粉] 사진으로 보는 전문조리용어 해설
쌀가루로 만든 가루로 납작한 국수를 말한다. 국물이 있는 국수가 아니라 볶은 국수이다.
분류중식 > 중식 조리용어 > 주식(主食)과 디저트용 요리
https://terms.naver.com/list.nhn?cid=42807&categoryId=42810
미분 [dust fines, powder, 微粉, びふん, パウダ-] 농업용어사전: 농촌진흥청
대기중에 부유되어 있는 미세한 고체상태의 물질을 말함.
https://terms.naver.com/list.nhn?cid=43658&categoryId=43658
미분 [fines, 微粉] 기계공학용어사전
최대 치수 44μ 이하의 입자로 이루어진 분말이다.
https://terms.naver.com/list.nhn?cid=44616&categoryId=44616
https://terms.naver.com/entry.nhn?docId=3570648&cid=58944&categoryId=58970
수학산책
미분
접선을 구하라
함수의 그래프를 보면, 부드럽게 굽어 보이는 그래프가 많다. 사인 함수를 비롯한 삼각함수도 그렇고, 지수함수, 로그함수, 무리함수, 유리함수, 다항함수까지 보통 접하는 함수의 그래프는 대개 쭉 뻗은 직선이기보다는 부드러운 곡선이다. 그런데 이런 곡선 위의 점을 하나 골라 그 주위를 확대해보면 의외의 세상을 만나는 수가 있다.
곡선과 가장 가까운 직선 - 접선
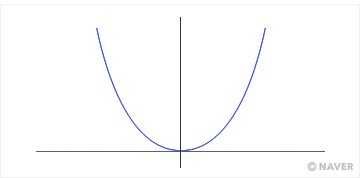
직선이 아닌 곡선 중 가장 간단한 것은 2차 함수의 그래프다. 그 중 가장 간단한 f(x)=x2의 그래프를 생각해 보자. 얼마나 간단한지, 대개 중고등학교 시절을 거치면서 무수히 그리는 경험을 한다. 이런 모양의 곡선을 포물선이라고 부르는데, 북한에서는 팔매선이라 부른다고 한다. 돌팔매질을 하면 돌이 그리는 자취가 2차 곡선의 모양이기 때문이다. 삼각함수나, 3차 함수 등이 아니고 하필 2차 곡선이어야 하는 이유도 미분과 적분으로 (공기 저항 등을 무시할 경우, 물리 법칙을 써서) 설명할 수 있는데, 그 얘기는 다음으로 미루고 여기서는 이 곡선을 확대해 보는 데 집중하기로 하자.
예를 들어 x=0.5를 제곱하면 0.25이다. 따라서 점 (0.5, 0.25)는 곡선 위에 있다. 이제 이 점을 중심으로 그래프를 일정 비율로 확대해 보자. 돋보기 들고, 컴퓨터 화면 확대해야겠다는 순진한 분은 없으리라 믿겠다. 예를 들어 2배, 4배, 8배, 16배, 32배 확대하면 아래 그림을 얻는다. 각 그림에서 가운데에 그린 네모를 가로, 세로 각각 두 배씩 확대하면 다음 그림이 나오도록 하였다. 점점 확대할수록 기울기가 1인 직선에 가까워지는 느낌을 받았는가?
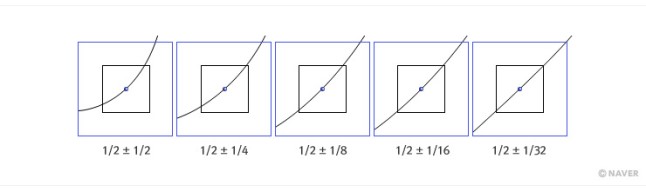
평균 변화율과 순간 변화율
이처럼 어떤 점 (L, f(L))을 중심으로 하여 확대하면 할수록 그래프가 어떤 고정된 직선에 가까워지는 경우, (단, y 축과 나란한 직선은 제외한다) x=L에서 ‘미분 가능하다’고 말하고, 그 고정된 직선을 접선이라 부른다. 즉, 미분 가능한 점 (L, f(L))에서의 접선은 그 점 근방에서 곡선과 가장 가까운 직선으로 이해할 수 있다. 그런데 이 접선은 어떻게 구할까? 이미 접선이 지나는 점 (L, f(L))을 알고 있으므로, 기울기만 구하면 된다.
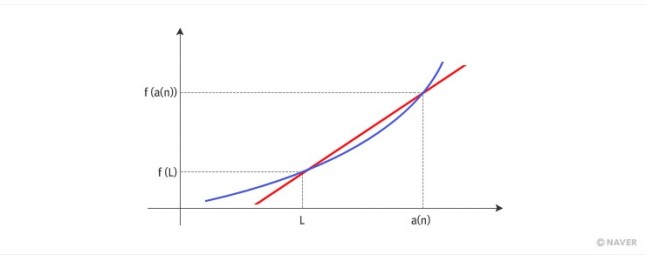
위그림은 미분 가능한 점 (L, f(L))을 중심으로 하여 상당히 확대한 그림이라고 하자. 곡선 위의 점 (a(n), f(a(n)))은 (L, f(L))과 멀어 보이지만, 엄청나게 확대한 그림이라면 실은 꽤 가까운 점이다. 이때 미분 가능하다고 했으므로, 이 두 점을 잇는 직선과, 함수의 그래프가 대단히 가깝다고 가정하고 있다. 두 점을 잇는 직선의 기울기는 y의 변화량f(a(n))-f(L)을 x의 변화량 a(n)-L로 나눈 값인
|
|
인데, 이 값을 두 점 (L, f(L)), (a(n), f(a(n)))의 평균 변화율이라 부른다. 구하고자 하는 접선의 기울기는, a(n)이 대단히 L에 가까울 때, 평균 변화율이 가까워지는 극한값이어야 할 것이다. 이 극한값을 L에서의 ‘순간 변화율’이라 부르는데, 다만 a(n)이 L인 경우는 애초부터 기울기를 생각할 수 없으므로 제외해야 한다. 예를 들어 f(x)=x2인 경우를 보자. a(n)이 L로 다가갈 때, 다음 극한을 생각하자는 얘기다. (다시 말하지만, a(n)은 L이 아니다.)
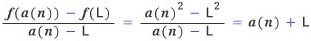 |
이고, a(n)이 L로 수렴한다고 했으므로, 극한값의 성질에 의해 이 값은 당연히 2L로 수렴한다. 따라서 x=L에서의 순간 변화율은 2L이다. L=1/2인 경우 위에서 그래프를 확대하며 짐작했던 것이 맞았음을 확인할 수 있다.
[네이버 지식백과] 미분 - 접선을 구하라 (수학산책)
리미트 공식에서부터 다음 포스트에 이어서....
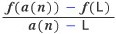
 [펌]네이버과학_수학포스터_대한수학회_9분할 181123.00:10.
[펌]네이버과학_수학포스터_대한수학회_9분할 181123.00:10.